本文是作者原创文章，欢迎转载，请注明出处 from:@Eric_Lai

写在前面

因为喜欢编程，但是苦于高考完之后的拍脑袋决定跑去学机械了，一直没有机会接受正统的计算机教育，所以一直对算法怀着一种“敬畏”的心情，觉得这是很难的一门课程而且对平时的工作没有很显著的作用。但是自从下定决心读研要转到和CS或者SE之后，就买了本书决定狠下心来啃啃它。《算法导论》，看着的确觉得很难，今天先讨论下看了的两个排序算法：插入排序和归并排序。

插入排序

说到插入排序，最经典的例子就是打牌的时候我们经常做的一个动作了（大家摸牌，而不是派发牌的时候）。对于正常人（奇葩不在我们的研究范围），如果是摸牌的话，一定会在摸牌的同时对手上的牌进行排序。一般而言，会按照非降序或者非升序进行排列（这里不用升序和降序是因为有可能会有两张相同的牌）。这里我们假设你用右手摸牌，左手持牌（牌按照非降序排列），那么你的整个动作流程应该是这样的：

  1. 右手从牌堆得最上方抽取一张牌；
  2. 与左手的牌从右向左一次进行比较；
  3. 将抽到的牌放到比它小的牌的右边且比它大的牌的左边；

下面，我们对这个流程进行抽象；牌堆–>待排列数组，左手的牌–>排列好的数组，右手的牌–>待排列数组当中的一个元素。那么我们需要做的就是将“右手的牌”和“左手的牌”（已经有序的数组）作一个比较直到找到合适的位置。伪码设计如下：

INSERTION(A){
    //A={x1,x2,..,xn}
    for j = 2 to n
    	key = A[j]
        i = j - 1
        while i > 0 and A[i] > key
            A[i+1] = A[i]
            i = i - 1
        A[i] = key
}

插入排序比较简单，这里就不给出具体的实现代码了。

归并算法

插入算法虽然可以解决问题，但是比较耗时，计算出来的平均效率是n的平方（至于怎么计算，需要进行算法分析，老实说我也没怎么看得很明白……囧）。对于很多复杂的问题，我们希望可以使用分治法思想来进行处理，分治模式一般分如下三个步骤：

  1. 分解原问题成若干个子问题，这些子问题是原问题的规模比较小的实例
  2. 解决这些子问题，递归的求解各个子问题
  3. 合并这些子问题的解成原问题的解

接下来我们要重点讨论的归并算法就完全遵循了分治法，直观上其操作如下：

  1. 分解待排列的n个数组元素，使之成为两个各具有n/2个元素数组
  2. 使用归并排序（递归调用本身）将两个子数组排成（非升序或者非降序）
  3. 合并两个已经排好序的子数组产生已排序的答案

这里的重点在与最后一步，合并排好的子数组。因为将一个数组一直二分下去，最后肯定会产生只有一个元素的数组。所以，其核心在于如何把子数组合成为一个有序的数组。具体的操作，还是用一个扑克牌的例子来描述：现在有两堆已经按非升序排好的牌（小的在上，大的在下）翻转放在桌子上（代表两个子数组），首先从两堆当中各取出最上层的一张，比较大小，将小的放出一边，另起一堆牌，该牌在牌堆的底。然后从被移走了一张的牌堆里再取出一张进行比较，重复上述操作，直到所有牌都到了第三堆。伪码的实现如下：

MERGE(A,p,q,r){
    //A={x1,x2,x3,...xn}
    //p q r is the subscript of A, and they are required p <= q < r
    n1 = q  - p + 1
    n2 = r - q
    let L[1...n1+1] and R[1...n2+1]
    for i = 1 to n1
    	L[i] = A[p+i-1]
    for j = n1 to n2
    	R[j] = A[q+j]
    //set the sentry
    L[n1+1] = ∞
    R[n2+1] = ∞
    i = 1
    j = 1
    for k = p to r
    	if L[k] = R[k]
        	A[k] = L[k]
        else
        	A[k] = R[k]
}

完成之后，我们就可以对这个函数进行调用了：

MERGE-SORT(A,p,r){
	if p < r
    	//four different result need to be solved
    	q = (p + r)/2
        MERGE-SORT(A,p,q)
        MERGE-SORT(A,q+1,r)
        MERGE(A,p,q,r)
}

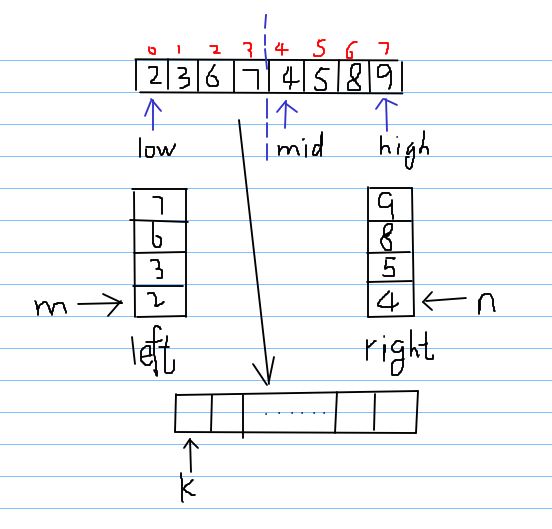
伪码有了，但是想要具体的用一种语言来实现还是有一定的差距的。 合并两个有子序列方法的具体实现流程可以如下图所示。我们假设有一个数组，分别有三个变量指向数组的开头、结尾和中间。然后新建两个数组left和right用来存放两个有序子序列（这里你需要决定将mid划分到前半部分还是后半部分）。然后再用三个变量分别指向两个数组的开头和一个排好序的数组的开头。把m，n指向的值拿出来比较，把小的放入到k指向的位置，k和m或者n向后移动，一直到m和n指向某一个数组到头。最后把另一个还有数的数组的数复制到k指向的数组里面。即可完成排序。

merge

下面给出在具体的Java实现代码：

package merge;

/**
 * 归并排序demo
 * @author ERIC_LAI
 */
public class Merge {
    /**程序的入口
     * @param args the command line arguments
     */
    public static void main(String[] args) {
        //随便定义的一组数,用于被排序
        int [] x = {2,1,4,3,0,5,6,3,8,4};
        //打印排序前的序列
        System.out.print("排列前:");
        for (int i = 0; i < x.length; i++) {
            System.out.print(x[i]+" ");
        }
        //数组的首下标
        int low = 0;
        //数组的末下标
        int high = x.length-1;
        //执行排序命令
        merge_sort(x, low, high);
        //打印排序后的数组
        System.out.print("\n排列后:");
        for (int i = 0; i < x.length; i++) {
            System.out.print(x[i]+" ");
        }
    }
    /**
     * 合并两个有序序列
     * @param array 输入一个包含两组已经排好的子序列的序列
     * @param low   首下标
     * @param mid   中间值下标
     * @param high  最后数值的下标
     */
    public static void merge(int [] array, int low, int mid, int high){
        //第一组子序列的大小
        int LEFT_SIZE = mid - low;
        //第二组子序列的下标
        int RIGHT_SIZE = high - mid + 1;
        //新建两个子序列
        int []left = new int[LEFT_SIZE];
        int []right = new int[RIGHT_SIZE];
        //m指向第一组子序列,n指向第二组子序列,k指向排好的序列
        int i, m = 0, n = 0, k = low;
        //将输入的序列的一半装入子序列
        for(i = low;i < mid;i++){
            left[i-low] = array[i];
        }
        //将输入序列的另一半装入另一个子序列
        //为了确保最后一个数值能被装入,这里需要用"<="
        for(i = mid;i <= high;i++){
            right[i-mid] = array[i];
        }
        //在两个子序列都没到头前,将两个子序列当中小得拿出来放到排好的序列当中
        while(m < LEFT_SIZE && n < RIGHT_SIZE){
            if(left[m] < right[n]){
                array[k++] = left[m++];
            }
            else{
                array[k++] = right[n++];
            }
        }
        //检测是哪一个子序列装完了,将剩下的子序列的内容复制到排好序列当中
        while (m < LEFT_SIZE) {            
            array[k++] = left[m++];
        }
        while (n < RIGHT_SIZE){
            array[k++] = right[n++];
        }
    }
    /**
     * 分解待排序的序列
     * @param array
     * @param low
     * @param high    
     */
    public static void merge_sort(int [] array, int low, int high){
        //检测是否二分到最小
        if (low < high) {
            //计算中间值
            int mid = (low + high) / 2;
            //二分前半部分
            merge_sort(array, low, mid);
            //二分后半部分
            merge_sort(array, mid+1, high);
            //排序两个有序子序列
            //我个人将mid归到第二个子序列里面,所以mid+1
            merge(array, low, mid+1, high);
        }
    }
}

最后，附上实验的结果图。

—result—merge